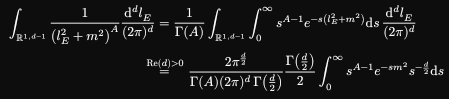How to properly align symbols in math mode When limits() function is used?

Questions
,
2

Your minimal example doesn’t compile, it’s also very big for what you are asking. See https://sscce.org/. And you don’t need the limits call. You can open an issue for this, as I don’t see any native solution.

Here is a hack:

#show math.attach: it => {
  let attachments = it.fields()
  let base = attachments.remove("base")
  if base != $=$.body { return it }
  let top = attachments.remove("t")
  if not attachments.values().all(x => x == none) { return it }
  top = $script(top)$
  base
  context {
    let width = measure(top).width
    let space = measure(" ").width

    // place(dx: -space * 2 - width / 2, dy: -1.15em, top)

    place(dx: -space - width / 2, dy: -1.15em, top)
    h(width / 2)
  }
}
Full example 
#set math.equation(numbering: "(1)")

#let dd = math.upright("d")
#let Re = $upright("Re")$

#show math.attach: it => {
  let attachments = it.fields()
  let base = attachments.remove("base")
  if base != $=$.body { return it }
  let top = attachments.remove("t")
  if not attachments.values().all(x => x == none) { return it }
  base
  top = $script(top)$
  context {
    let width = measure(top).width
    let w = measure(" ").width

    // place(dx: -w * 2 - width / 2, dy: -1.15em, top)

    place(dx: -w - width / 2, dy: -1.15em, top)
    h(width / 2)
  }
}

#[
  #set math.equation(numbering: none)
  $
    integral_(RR^(1, d - 1)) frac(1, (l_E^2 + m^2)^A) frac(dd^d l_E, (2 pi)^d)
    &= 1 / Gamma(A) integral_(RR^(1, d - 1)) integral_0^oo s^(A - 1) e^(-s(l_E^2 + m^2)) dd s thin frac(dd^d l_E, (2 pi)^d) \
    &=^(Re(d) > 0) (2 pi^(d / 2)) / (Gamma(A) (2 pi)^d thin Gamma(d / 2)) Gamma(d / 2) / 2 integral_0^oo s^(A - 1) e^(-s m^2) s^(-d / 2) dd s \
  $
]

image