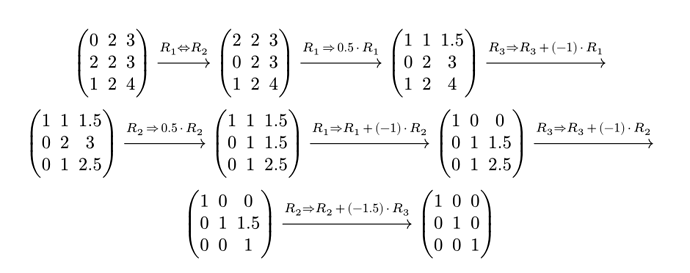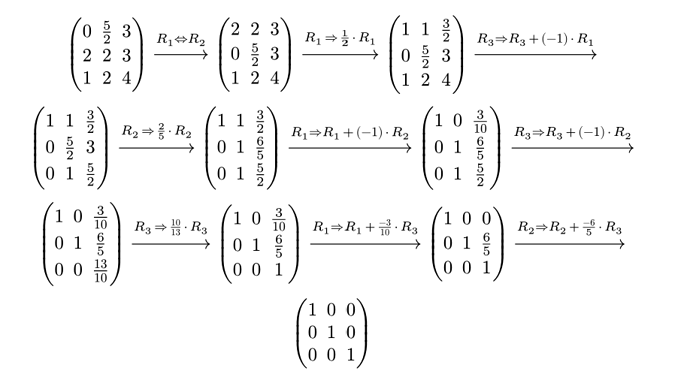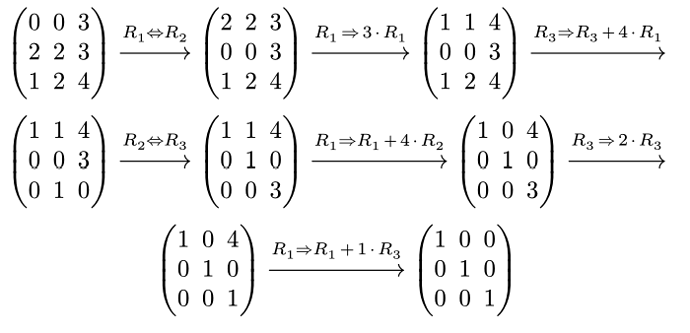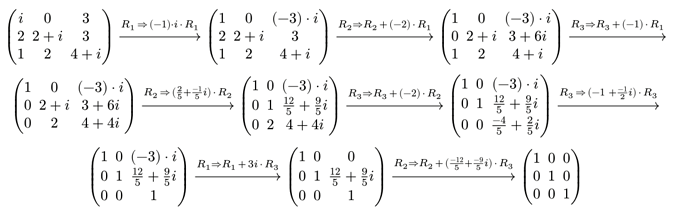While procrastinating doing my linear algebra homework I wrote a little script that automatically ranks matrices for you.
I broke it down into 2 parts, one function that calculates the steps:
#let rank(mat, mathods) = {
let (add, mul, negate, invert, is-zero, is-one) = mathods;
let steps = (("start", mat),)
for i in range(mat.len()) {
if is-zero(mat.at(i).at(i)) {
let brk = false
for j in range(i+1, mat.len()) {
if not is-zero(mat.at(j).at(i)) {
(mat.at(i), mat.at(j)) = (mat.at(j), mat.at(i))
steps.push(("switch", mat, i, j))
brk = true
break
}
}
if not brk {
// return steps
panic("unsolvable")
}
}
if not is-one(mat.at(i).at(i)) {
let lambda = invert(mat.at(i).at(i))
mat.at(i) = mat.at(i).map(x => mul(x, lambda))
steps.push(("mul", mat, i, lambda))
}
for j in range(mat.len()) {
if i == j {
continue
}
let lambda = negate(mat.at(j).at(i))
if is-zero(lambda) {
continue
}
mat.at(j) = mat.at(j).enumerate().map(((k,x)) => add(x, mul(mat.at(i).at(k), lambda)))
steps.push(("add", mat, i, j, lambda))
}
}
return steps
}
And another that renders them:
#let render(steps, methods, items-per-line: 3) = {
let (render, requires-brackets) = methods
let render-quotient(lambda) = if requires-brackets(lambda) { $(#render(lambda))$ } else { render(lambda) }
$
#for (item, (case, mat, ..step)) in steps.enumerate() {
if case == "start" {
// nothing
} else if case == "switch" {
let (i,j) = step
xarrow($R_#(i+1) <=> R_#(j+1)$)
} else if case == "mul" {
let (i,lambda) = step
xarrow($R_#(i+1) op(=>) #render-quotient(lambda) op(dot) R_#(i+1)$)
} else if case == "add" {
let (i,j,lambda) = step
xarrow($R_#(j+1) => R_#(j+1) op(+) #render-quotient(lambda) op(dot) R_#(i+1)$)
}
if calc.rem(item, items-per-line) == 0 {
linebreak()
}
math.mat(..mat.map(row => row.map(render)))
}
$
}
Both of the functions take in a methods parameter as a sort of pseudo-interface system, these are methods for performing arithmetic and rendering whatever field you chose. For example, here is the trivial implementation for these methods using floats:
#let float-methods = (
add: (x,y) => x + y,
mul: (x,y) => x * y,
negate: x => -x,
invert: x => 1/x,
is-zero: x => x == 0,
is-one: x => x == 1,
render: x => $#x$,
requires-brackets: x => x < 0
)
Here’s an example usage of it:
#let steps = rank(
(
(0,2,3),
(2,2,3),
(1,2,4),
),
float-methods
)
#render(steps, float-methods)
Which produces:
But off course the second you start messing with fractions everything goes off the rails:
#let steps = rank(
(
(0,2.5,3),
(2,2,3),
(1,2,4),
),
float-methods
)
#render(steps, float-methods)
I made an alternative implementation that stores rational numbers as pairs:
#let create-rational(n,m) = {
let gcd = calc.gcd(n,m)
return (int(n/gcd), int(m/gcd))
}
#let rational-methods = (
add: ((x,y), (a,b)) => create-rational(x*b + a*y, b*y),
mul: ((x,y), (a,b)) => create-rational(x*a, y*b),
negate: ((x,y)) => (-x, y),
invert: ((x,y)) => if x >= 0 { (y,x) } else { (-y, -x) },
is-zero: ((x,y)) => x == 0,
is-one: ((x,y)) => x == y,
render: ((x,y)) => if y == 1 { $#x$ } else { $#x/#y$ },
requires-brackets: ((x,y)) => y == 1 and x < 0
)
It requires some updates but now the result is a lot more readable:
#let steps = rank(
(
((0,1),(5,2),(3,1)),
((2,1),(2,1),(3,1)),
((1,1),(2,1),(4,1)),
),
rational-methods
)
#render(steps, rational-methods)
I also made implementations for the complex numbers and modular fields which work similarly:
#let mod-methods(p) = (
add: (x,y) => calc.rem(x + y, p),
mul: (x,y) => calc.rem(x * y, p),
negate: x => calc.rem(p - x, p),
invert: x => for y in range(p) {
if calc.rem(x+y,p) == 0 {
return y
}
},
is-zero: x => calc.rem(x,p) == 0,
is-one: x => calc.rem(x,p) == 1,
render: x => $#x$,
requires-brackets: x => false
)
#let steps = rank(
(
(0,2.5,3),
(2,2,3),
(1,2,4),
),
mod-methods(5)
)
#render(steps, mod-methods(5))
// this one takes in another implementation so that you could choose
// whether to use rationals or floating point numbers to represent
// the real and imaginary parts.
#let complex-methods(methods) = {
let (add, mul, negate, invert, is-zero, is-one, render, requires-brackets) = methods
return (
add: ((x,y), (a,b)) => (add(x,a), add(y,b)),
mul: ((x,y), (a,b)) => (add(mul(x,a),negate(mul(y,b))), add(mul(x,b),mul(y,a))),
negate: ((x,y)) => (negate(x), negate(y)),
invert: ((x,y)) => (
mul(
x,
invert(
add( mul(x,x), mul(y,y) )
)
),
mul(
negate(y),
invert(
add( mul(x,x), mul(y,y) )
)
),
),
is-zero: ((x,y)) => is-zero(x) and is-zero(y),
is-one: ((x,y)) => is-one(x) and is-zero(y),
render: ((x,y)) =>
if is-zero(y) { render(x) }
else if is-zero(x) {
if is-one(y) {
$i$
} else if requires-brackets(y) {
$(#render(y)) dot i$
} else {
$#render(y)i$
}
} else {
$#render(x) + #if is-one(y) {
$i$
} else if requires-brackets(y) {
$(#render(y)) dot i$
} else {
$#render(y)i$
}$
},
requires-brackets: ((x,y)) => (not is-zero(x) and not is-zero(y)) or requires-brackets(x)
)
}
#let steps = rank(
(
(((0,1),(1,1)), ((0,1), (0,1)), ((3,1), (0,1))),
(((2,1),(0,1)), ((2,1), (1,1)), ((3,1), (0,1))),
(((1,1),(0,1)), ((2,1), (0,1)), ((4,1), (1,1))),
),
complex-methods(rational-methods)
)
#render(steps, complex-methods(rational-methods))
Theoretically it should be possible to create an implementation that supports variables, but I don’t really have enough time (or patience) for that at the moment.
I think that this isn’t really a useful enough thing to make an entire package out of it, but I figured I’d post it here in case anyone who does find it useful stumbles across it.