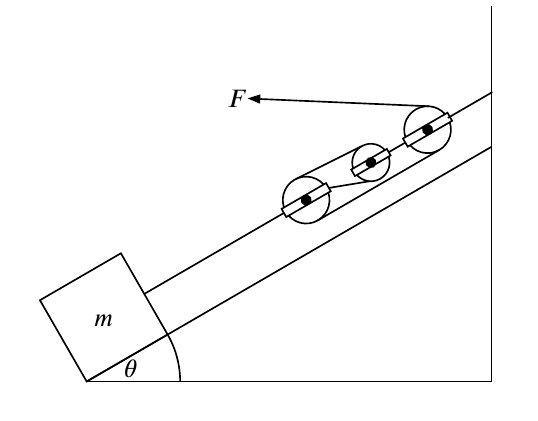
I want to create a diagram of pulleys on an inclined plane, I draw every thing in (x ,y) plane and then rotate it. However, the anchor just shifts all. How I can solve this?
3 Likes
Can you share the code you used? I tried to reproduce this, but e.g. the following example works:
#import "@preview/cetz:0.3.0"
// #show: rotate.with(15deg, reflow: true)
#cetz.canvas({
import cetz.draw: *
rotate(z: 15deg)
circle((0,0), name: "circle1")
circle((3,0), name: "circle2")
line("circle1.south", "circle2.south")
})
whether rotated within the canvas or afterwards (using the commented line), the line is tangent to both circles, i.e. the anchors were transformed and “south” is not “towards the bottom of the page”; the whole diagram is unchanged except for it being rotated as a whole.
(I now realize that your title asks “without affecting the anchors of the elements”; the way I would view this situation is that your anchors already were “not affected” and stayed at the original rotation – regardless, I think we mean the same thing)
So since I noticed that you using anchors such as “east” is not completely correct, and since I had some time this evening, I tried to calculate the correct tangent points and made this pulley example:
Pulley example code
#set page(width: auto, height: auto, margin: 0.3cm)
#import "@preview/cetz:0.3.0"
#let tangent((cx1, cy1, r1), (cx2, cy2, r2)) = {
let (cx, cy, r) = (cx2 - cx1, cy2 - cy1, r2 - r1)
let tmp = cx*cx + cy*cy - r*r
if tmp < 0 { return }
let tmp = calc.sqrt(tmp)
let denom = cx*cx + cy*cy
let a = (cy*tmp + cx*r2 - cx*r1) / denom
let b = -(cx*tmp - cy*r2 + cy*r1) / denom
let c = -((cx1*cy2 - cx2*cy1)*tmp + (cy1*cy2 - cy1*cy1 + cx1*cx2 - cx1*cx1)*r2 + (-cy2*cy2 + cy1*cy2 - cx2*cx2 + cx1*cx2)*r1) / denom
let c1 = -((cy1*cy2 - cy1*cy1 + cx1*cx2 - cx1*cx1)*tmp + (cx2*cy1 - cx1*cy2)*r2 + (cx1*cy2 - cx2*cy1)*r1) / denom
let c2 = -((cy2*cy2 - cy1*cy2 + cx2*cx2 - cx1*cx2)*tmp + (cx2*cy1 - cx1*cy2)*r2 + (cx1*cy2 - cx2*cy1)*r1) / denom
let x1 = -(a*c - b*c1)/(a*a + b*b)
let y1 = -(a*c1 + b*c)/(a*a + b*b)
let x2 = -(a*c - b*c2)/(a*a + b*b)
let y2 = -(a*c2 + b*c)/(a*a + b*b)
((x1, y1), (x2, y2))
}
#let specific-tangent((x1, y1, r1), (x2, y2, r2), p1, p2) = {
assert(p1 in ("a", "b"))
assert(p2 in ("a", "b"))
if p1 == "b" { r1 *= -1 }
if p2 == "b" { r2 *= -1 }
tangent((x1, y1, r1), (x2, y2, r2))
}
#let tangents(c1, c2) = {
// in case there is not a single tangent we want to return an empty array instead of none
// so put one here so that everything else is joined with it
()
for p1 in ("a", "b") {
for p2 in ("a", "b") {
let t = specific-tangent(c1, c2, p1, p2)
if t != none { (t,) }
}
}
}
#cetz.canvas({
import cetz.draw: *
rotate(-65deg)
let pulleys = (
(0, 9, 0),
(5, 15, 1),
(5, 12, 0.8),
(5, 9, 1),
(5, 10, 0),
)
for (x, y, r) in pulleys {
circle((x, y), radius: r)
}
line(..specific-tangent(pulleys.at(0), pulleys.at(1), "a", "a"), mark: (start: ">"))
line(..specific-tangent(pulleys.at(1), pulleys.at(3), "a", "a"))
line(..specific-tangent(pulleys.at(3), pulleys.at(2), "a", "a"))
line(..specific-tangent(pulleys.at(2), pulleys.at(4), "a", "a"))
// for t in tangents(pulleys.at(1), pulleys.at(2)) {
// line(..t)
// }
})
It’s not exactly the answer to what your problem is about, but I wanted to share it anyway.
This is the code I used to produce a pulley:
#let pulley(radius: 1, ..args) = {
let kwargs = args.named()
args = args.pos()
let exkwargs = (circle: (:), rect: (:))
draw.group(..kwargs, {
if "name" in kwargs.keys() {
exkwargs.insert("circle", (name: "circle"))
exkwargs.insert("rect", (name: "rect"))
}
draw.circle(radius: radius, ..args, ..exkwargs.circle)
draw.on-layer(1, {draw.circle(radius: 0.1, fill: black, ())})
draw.rect((to: (), rel: (-0.2 * radius, -1.1 * radius)),
fill: white, (rel: (0.4 * radius, 2 * 1.1 * radius)), ..exkwargs.rect)
})
And the code for the diagram
#canvas({
import draw: *
let pulley = pulley.with(radius: 0.5)
group(
name: "inclined",
{
set-origin((0, 0))
rotate(-60deg)
line(name: "floor", (0, 0), (0, 10))
line(name: "wall", (to: "floor.end", rel: (-3, 0)), (rel: (5, 0)), stroke: none)
rect(name: "o", (to: "floor.mid", rel: (0, -5)), (rel: (-2, 2)))
line(name: "x1", "o.north", ((), "|-", "floor.end"), stroke: none)
pulley(name: "p1", (rel: (0, -1), to: "x1.end"))
pulley(name: "p2", radius: 0.4, (rel: (0, -2.4), to: "x1.end"))
pulley(name: "p3", (rel: (0, -4), to: "x1.end"))
on-layer(
-1,
{
line(
(to: "p3", rel: (0, 0.5)),
(element: "p2.circle", point: "p3.north", solution: 1),
)
line(
(to: "p2", rel: (-0.4, 0)),
(element: "p3.circle", point: (to: "p2", rel: (-0.4, 0)), solution: 1),
)
line((to: "p2", rel: (0, 0.4)), (to: "p1", rel: (0, -0.5)))
line((to: "p3", rel: (0.5, 0)), (to: "p1", rel: (0.5, 0)))
line(
name: "F",
(
element: "p1.circle",
point: (to: (to: "p1", rel: (-0.5, 0)), rel: (-2, -3)),
solution: 2,
),
(to: (to: "p1", rel: (-0.5, 0)), rel: (-2, -3)),
mark: (end: ">", fill: black),
)
line((to: "p3", rel: (0, 0.5)), "o.north")
},
)
circle(name: "p1:N", (to: "p1", rel: (0, 0.5)), stroke: none)
},
)
line(
name: "floor",
"inclined.floor.start",
((), "-|", "inclined.floor.end"),
"inclined.floor.end",
)
line(("inclined.floor.start", "-|", "inclined.floor.end"), (rel: (0, 8)))
line("inclined.p1:N", (rel: (30deg, 1.1)))
content("inclined.o", $m$)
content("inclined.F.end", anchor: "east", $F$)
cetz.angle.angle(
"inclined.floor.start",
(to: "floor.start", rel: (5, 0)),
"inclined.floor.end",
label: $theta$,
radius: 2,
)
})
In the meantime, I temporary fixed the issue by change the coordinate p1.south to (to: "p1", rel: (0, -0.5)) instead, that’s why my code is so cursed.
This is the output by the way:
