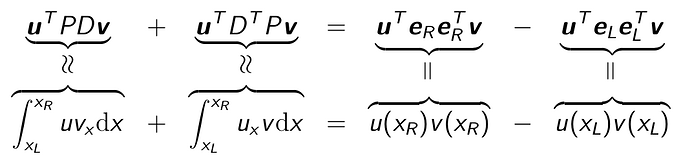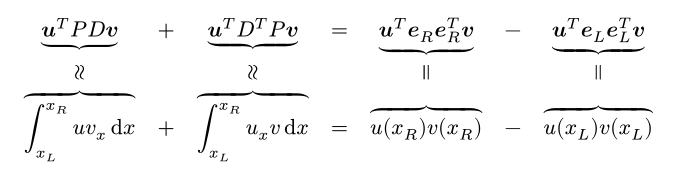How can I align multiple terms in a multi-line block equation?

[lampert]

I would like to have a multi-line equation, where the different terms in each equation of the different lines are aligned centrally, such that I can relate them to each other with underbrace and overbrace. The result should look like similar to this:

which I created in LaTeX with

\begin{equation*}
	\begin{array}{ccccccc}
		\underbrace{\bm u^TPD\bm v}_{\vapprox} &+& \underbrace{\bm u^TD^TP\bm v}_{\vapprox} &=& \underbrace{\bm u^T\bm e_R\bm e_R^T\bm v}_{\veq} &-& \underbrace{\bm u^T\bm e_L\bm e_L^T\bm v}_{\veq}\\
		\overbrace{\displaystyle\int_{x_L}^{x_R} uv_x\tr dx} &+& \overbrace{\displaystyle\int_{x_L}^{x_R} u_xv\tr dx} &=& \overbrace{u(x_R)v(x_R)} &-& \overbrace{u(x_L)v(x_L)}
	\end{array}
\end{equation*}

I tried two options, which are both not satisfying to me:

1. using alignment points &, but this does not center the terms,
2. put everything in a matrix with no delimiter, but this feels a bit hacky and the integrals are too small like they are in inline equations.

Code for first option:

$ underbrace(bold(u)^T P D bold(v), vapprox) &+& underbrace(bold(u)^T D^T P bold(v), vapprox) &=&
  underbrace(bold(u)^T bold(e)_R bold(e)_R^T bold(v), veq) &-& underbrace(bold(u)^T bold(e)_L bold(e)_L^T bold(v), veq) \
  overbrace(integral_(x_L)^(x_R) u v_x dif x) &+& overbrace(integral_(x_L)^(x_R) u_x v dif x) &=&
  overbrace(u(x_R) v(x_R)) &-& overbrace(u(x_L) v(x_L)) $

Code for second option:

#set math.mat(delim: none)
$ mat(
    underbrace(bold(u)^T P D bold(v), vapprox), +, underbrace(bold(u)^T D^T P bold(v), vapprox), =, underbrace(bold(u)^T bold(e)_R bold(e)_R^T bold(v), veq), -, underbrace(bold(u)^T bold(e)_L bold(e)_L^T bold(v), veq) ;
    overbrace(integral_(x_L)^(x_R) u v_x dif x), +, overbrace(integral_(x_L)^(x_R) u_x v dif x), =, overbrace(u(x_R) v(x_R)), -, overbrace(u(x_L) v(x_L))
) $,

where both of these use

#let vapprox = (rotate(90deg)[$approx$])
#let veq = (rotate(90deg)[$=$])

See also this document: https://typst.app/project/rOQLu8z7tgsvdfAwf8MAst
What would be the best way to achieve this?

[lampert]

Of course I could use display in the second option to enlarge the integrals and this already comes close to what I want, but I am still wondering if there is a better option without mat.

[quachpas]

I think you can use a grid for that!

[Eric]

Using a grid will probably lead to misaligned baselines. I may have overdone it a bit, but here is a function for math-grids with custom gutter and alignments. It even allows passing arrays for alignments (like in default grids), and overriding the alignment of specific cells by wrapping them with the standard align element.

Function Definition

#let mgrid(align: center, gutter: 1em, eq) = context {
  if eq.func() != [].func() {
    // Body is just a single element, so leave it as is.
    return eq
  }

  // Split body at linebreaks and alignment points.
  let lines = eq.children.split(linebreak()).map(line => line.split($&$.body).map(array.join))

  // Calculate width of each column.
  let widths = ()
  for line in lines {
    for (i, part) in line.enumerate() {
      let width = measure(math.equation(block: true, numbering: none, part)).width
      if i >= widths.len() {
        widths.push(width)
      } else {
        widths.at(i) = calc.max(widths.at(i), width)
      }
    }
  }

  // Resolve alignment for each column.
  let aligns = range(widths.len()).map(i => {
    if type(align) == alignment { align }
    else if type(align) == array { align.at(calc.rem(i, align.len())) }
    else { panic("expected alignment or array as 'align'") }
  })

  // Try to flatten sequence elements (to allow access to an underlying align
  // element for overriding the alignment of single parts).
  let flatten(seq) = {
    if type(seq) != content or seq.func() != [].func() {
      return seq
    }
    let children = seq.children.filter(c => c != [ ])
    if children.len() == 1 { children.first() } else { seq }
  }

  // Display parts centered in each column and add gutter.
  let layout-line(line) = {
    if line.len() < widths.len() {
      line += (none,) * (widths.len() - line.len())
    }
    
    line.zip(widths, aligns).map(((part, width, align)) => {
      let part = flatten(part)
      let part-width = measure(math.equation(block: true, numbering: none, part)).width
      let delta = width - part-width

      // Check if alignment is overridden.
      if type(part) == content and part.func() == std.align {
        align = part.alignment.x
      }
      
      let (start, end) = if align == center {( h(delta/2), h(delta/2) )}
                         else if align == left {( none, h(delta) )}
                         else if align == right {( h(delta), none )}

      start + part + end
    }).join(h(gutter))
  }

  lines.map(layout-line).join(linebreak())
}

For your case, the use then looks like this:

// Use display math here so that the bounds are correct.
#let vapprox = rotate(90deg, $ approx $)
#let veq = rotate(90deg, $ = $)

$ mgrid(gutter: #1em,
    underbrace(bold(u)^T P D bold(v))
      & + & underbrace(bold(u)^T D^T P bold(v))
      & = & underbrace(bold(u)^T bold(e)_R bold(e)_R^T bold(v))
      & - & underbrace(bold(u)^T bold(e)_L bold(e)_L^T bold(v)) \

    vapprox && vapprox && veq && veq \
  
    overbrace(integral_(x_L)^(x_R) u v_x dif x)
      & + & overbrace(integral_(x_L)^(x_R) u_x v dif x)
      & = & overbrace(u(x_R) v(x_R))
      & - & overbrace(u(x_L) v(x_L)) \
) $

[lampert]

Wow, that’s pretty awesome @Eric. This is a function I will likely use more often in the future. Really helpful. Thanks a lot for your effort @Eric!