How can I draw strictly diagonally dominant matrices with ellipses?

infinitymdm · November 11, 2024, 5:08pm

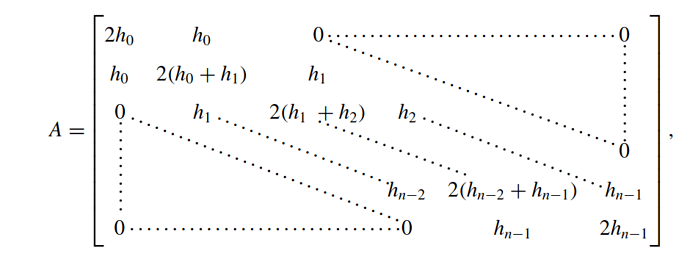
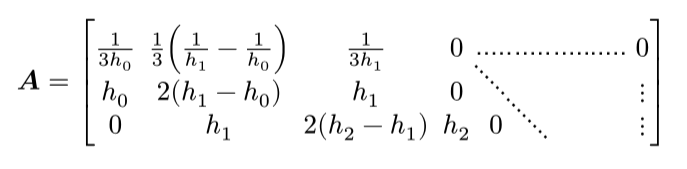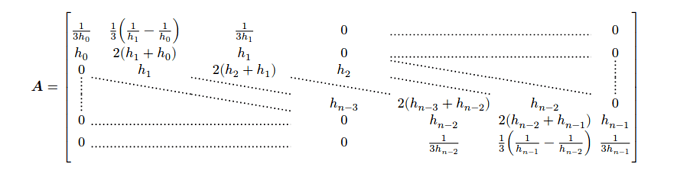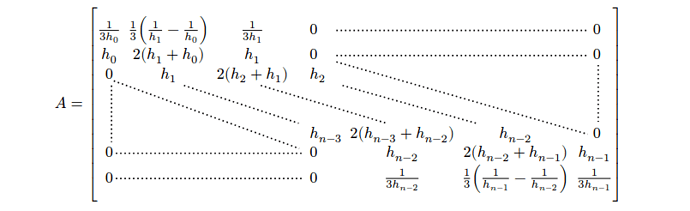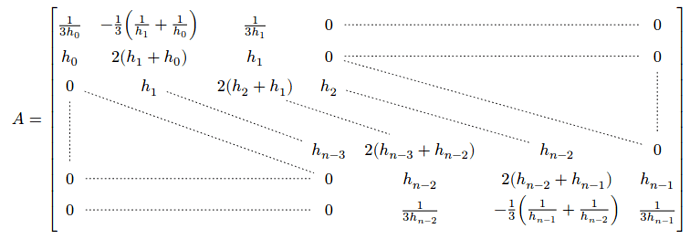Hi folks! I’m trying to more or less replicate this matrix from a textbook (with slightly different expressions):

The expressions are easy, but I’m having some difficulty with the upper and lower triangular regions. I’d like to find a way to replicate the way this text shows it, with ellipses indicating where the zeros are, but I’m not (yet) experienced enough with typst to figure it out.

Here’s the source I’m using for my not-yet-complete poor man’s version of this:

$
  bold(A) = mat(delim: #("[", "]"),
    1/(3 h_0), 1/3 (1/h_1 - 1/h_0), 1/(3 h_1),    0,   dots.h,    dots.h,   dots.h, dots.h, 0     ;
    h_0,       2 (h_1 - h_0),       h_1,          0,   dots.down, ,         ,       ,       dots.v;
    0,         h_1,                 2(h_2 - h_1), h_2, 0,         dots.down,,       ,       dots.v;
  )                                                                                                                                                                            $

And here’s how that looks (again, don’t worry about the expressions, just the triangular portion with the zeros):

The separated groups of dots are obviously not ideal. I can’t help but feel there’s a better way to do this. Any advice for me?

Sinthoras · November 11, 2024, 7:01pm

A bad solution which abuses the line and space commands is

#[
#set line(stroke: (dash: "dotted"))
#let horizontal = { 
  line(start: (-0.25em, 0.3em), end: (1.0em, 0.3em)) 
  h(-0.17em)
}
$
  bold(A) = mat(delim: #("[", "]"),
    1/(3 h_0), 1/3 (1/h_1 - 1/h_0), 1/(3 h_1),    0,   #horizontal,    #horizontal,   #horizontal, #horizontal, 0     ;
    h_0,       2 (h_1 - h_0),       h_1,          0,   #line(start: (-0.4em, -0.9em), end: (0.7em, 0.2em)), ,         ,       ,       dots.v;
    0,         h_1,                 2(h_2 - h_1), h_2, 0,         #line(start: (-0.5em, -0.5em), end: (1em, 1em)),,       ,       dots.v;
  )                                                                                                          $
]

which results in

infinitymdm · November 11, 2024, 7:11pm

Unfortunately, I don’t think that will work well for the completed matrix. I have several columns that are a tad wider than the rest along the diagonal. Here’s the complete matrix:

$                                                                                                                                                                                                                                            
    bold(A) = mat(delim: #("[", "]"),                                                                                                                                                                                                        
        1/(3 h_0), 1/3 (1/h_1 - 1/h_0), 1/(3 h_1),    0,         dots.h,               dots.h,                      0            ;                                                                                                           
        h_0,       2 (h_1 + h_0),       h_1,          0,         dots.h,               dots.h,                      0            ;                                                                                                           
        0,         h_1,                 2(h_2 + h_1), h_2,       dots.down,            ,                            dots.v       ;                                                                                                           
        dots.v,    dots.down,           dots.down,    dots.down, dots.down,            dots.down,                   dots.v       ;                                                                                                           
        dots.v,    ,                    dots.down,    h_(n-3),   2(h_(n-3) + h_(n-2)), h_(n-2),                     0            ;                                                                                                           
        0,         dots.h,              dots.h,       0,         h_(n-2),              2(h_(n-2) + h_(n-1)),        h_(n-1)      ;                                                                                                           
        0,         dots.h,              dots.h,       0,         1/(3 h_(n-2)),        1/3 (1/h_(n-1) - 1/h_(n-2)), 1/(3 h_(n-1));                                                                                                           
                                                                                                                                                                                                                                             
    )                                                                                                                                                                                                                                        
$

That ^ looks like this:

I’ll give your solution a go as a quick fix. I may be able to fiddle with it until it looks ok this time, but ideally there’s a more flexible solution.

infinitymdm · November 11, 2024, 8:13pm

Using your solution I was able to get a semi-acceptable result, but it’s pretty ugly:

Here’s the code:

#let (x0, x1, y0, y1) = (-0.5em, 6.6em, -0.2em, 1em)
#let v_line = line(stroke: (dash: "dotted"), start: (0em, y0), end: (0em, y1))
#let h_line = line(stroke: (dash: "dotted"), start: (x0, 0.5em), end: (x1, 0.5em))
#let d_line = line(stroke: (dash: "dotted"), start: (x0, y0), end: (x1, 1em))
$
    bold(A) = mat(delim: #("[", "]"),
        1/(3 h_0), 1/3 (1/h_1 - 1/h_0), 1/(3 h_1),    0,         #h_line,              #h_line,                     0            ;
        h_0,       2 (h_1 + h_0),       h_1,          0,         #h_line,              #h_line,                     0            ;
        0,         h_1,                 2(h_2 + h_1), h_2,       #d_line,              ,                            #v_line      ;
        #v_line,   #d_line,             #d_line,      #d_line,   #d_line,              #d_line,                     #v_line      ;
        #v_line,   ,                    #d_line,      h_(n-3),   2(h_(n-3) + h_(n-2)), h_(n-2),                     0            ;
        0,         #h_line,             #h_line,      0,         h_(n-2),              2(h_(n-2) + h_(n-1)),        h_(n-1)      ;
        0,         #h_line,             #h_line,      0,         1/(3 h_(n-2)),        1/3 (1/h_(n-1) - 1/h_(n-2)), 1/(3 h_(n-1));
    )
$

This also has the undesirable side effect of making the matrix very wide, since the lines are now the widest elements in most columns. I understand that some additional width is inevitable in order to make sure all the diagonal lines end up parallel, but the way things are spaced here makes the matrix hard to visually parse. I’m not sure how to solve this.

infinitymdm · November 11, 2024, 9:27pm

Well, I solved some problems (and created several new ones) using a really nasty hack: I’m using almost entirely negative starting positions for each line, as that doesn’t seem to affect the column width. Look if you dare.

awful hacky code

// This is perhpas the most horrific typst code I've written                                                                               
#let v_line_1 = line(stroke: (dash: "dotted"), start: (0.3em, -2.6em), end: (0.3em, 1em))                                                  
#let v_line_2 = line(stroke: (dash: "dotted"), start: (0.5em, -2.6em), end: (0.5em, 1em))                                                  
#let h_line_1 = line(stroke: (dash: "dotted"), start: (-12em, 0em), end: (0em, 0em))                                                       
#let d_line_1 = line(stroke: (dash: "dotted"), start: (-11.6em, -4.6em), end: (0.2em, -0.3em))                                             
#let h_line_2 = line(stroke: (dash: "dotted"), start: (-16em, 0em), end: (0em, 0em))                                                       
#let d_line_2 = line(stroke: (dash: "dotted"), start: (-16em, -4.6em), end: (0em, 0em))                                                    
#let d_line_3 = line(stroke: (dash: "dotted"), start: (-8em, -1.2em), end: (-0.7em, 1.2em))                                                
#let d_line_4 = line(stroke: (dash: "dotted"), start: (-9em, -1.2em), end: (-1em, 1.2em))                                                  
#let d_line_5 = line(stroke: (dash: "dotted"), start: (-11em, -1.2em), end: (-2.5em, 1.2em))                                               
$                                                                                                                                          
    A = mat(delim: #("[", "]"),                                                                                                            
        1/(3 h_0), 1/3 (1/h_1 - 1/h_0), 1/(3 h_1),            &0,         ,                     ,                  #h_line_2 0            ;
        h_0,       2 (h_1 + h_0),       h_1,                  &0,         ,                     ,                  #h_line_2 0            ;
        0,         h_1,                 2(h_2 + h_1),         &h_2,       ,                     ,                                         ;
        ,          ,                    ,                     &,          ,                     ,                                         ;
        ,          ,                    ,           #d_line_3 &,#d_line_4 ,           #d_line_5 ,                            #v_line_2    ;
        #v_line_1, ,                    ,                     &h_(n-3),   2(h_(n-3) + h_(n-2)), h_(n-2),           #d_line_2 0            ;
        0,         ,                    , #d_line_1 #h_line_1 &0,         h_(n-2),              2(h_(n-2) + h_(n-1)),        h_(n-1)      ;
        0,         ,                    ,           #h_line_1 &0,         1/(3 h_(n-2)),        1/3 (1/h_(n-1) - 1/h_(n-2)), 1/(3 h_(n-1));
                                                                                                                                           
    )                                                                                                                                      
$

That renders like this:

Of course, now I have the following new problems:

columns with lines in front of them get extra spacing for some reason (thus the alignment in col 4)
the diagonal lines aren’t parallel at all

I really hope there’s a better way to do this.

ian · November 13, 2024, 5:29pm

This looks like a perfect job for fletcher: fletcher – Typst Universe

I’m not fully sure how you would use it to integrate with the matrix itself. You may need to redefine the mat command, or potentially include the matrix inside the diagram. But if you want fancy lines connecting things, fletcher is the place to start.

infinitymdm · November 14, 2024, 4:01am

I gave fletcher a try. It definitely produces a much better result, but still not quite perfect. Here’s what I ended up with:

$
    A = mat(delim: #("[","]"),
        #diagram(
            spacing: 0pt,
            node((0,0), $1/(3 h_0)$),     node((1,0), $-1/3 (1/h_1 + 1/h_0)$), node((2,0), $1/(3 h_1)$),                 node((3,0), $0$),             edge((3,0), (6,0), "dotted"),                                                     node((6,0), $0$),
            node((0,1), $h_0$),           node((1,1), $2 (h_1 + h_0)$),        node((2,1), $h_1$),                       node((3,1), $0$),             edge((3,1), (6,1), "dotted"),                                                     node((6,1), $0$),
            node((0,2), $0$),             node((1,2), $h_1$),                  node((2,2), $2(h_2 + h_1)$, defocus: -1), node((3,2), $h_2$),           edge((3,1), (6,4), "dotted"),                                                     edge((6,1), (6,4), "dotted"),
            edge((0,2), (0,5), "dotted"), edge((0,2), (3,5), "dotted"),        edge((1,2), (3,4), "dotted"),             edge((2,2), (4,4), "dotted"), edge((3,2), (5,4), "dotted"),                     node((5,3), height: 2em),
                                                                                                                         node((3,4), $h_(n-3)$),       node((4,4), $2(h_(n-3) + h_(n-2))$, defocus: -1), node((5,4), $h_(n-2)$),                      node((6,4), $0$),
            node((0,5), $0$),             edge((0,5), (3,5), "dotted"),                                                  node((3,5), $0$),             node((4,5), $h_(n-2)$),                           node((5,5), $2(h_(n-2) + h_(n-1))$),         node((6,5), $h_(n-1)$),
            node((0,6), $0$),             edge((0,6), (3,6), "dotted"),                                                  node((3,6), $0$),             node((4,6), $1/(3 h_(n-2))$),                     node((5,6), $-1/3 (1/h_(n-1) + 1/h_(n-2))$), node((6,6), $1/(3 h_(n-1))$)
        )
    )
$

which looks like this:

I still feel that there ought to be a better way to do this sort of thing, but this is admittedly a pretty niche use case. For now this is good enough.