How can I underbrace only part of a matrix?

Questions
1

How would I underbrace a part of a matrix like in this image?
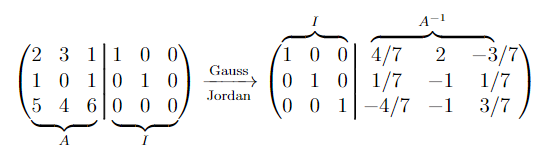
image

1 Like
2

There is no nice way to mix multiple underbraces together, so you will have to get creative with stack or grid. Here is one such PoC (for matrices with the same width each side, edit: see below for a more complete approach):

#let under-mat(matrix, left, right) = context {
  let width = measure(matrix).width / 2 - 10pt
  let lspace = math.underbrace(h(width), left)
  let rspace = math.underbrace(h(width), right)
  
  $
    #stack(
      spacing: -0.75em,
      matrix,
      grid(columns: 2, lspace, rspace)
    )
  $
}


#under-mat(
  $ mat(augment: #3, 2, 3, 1, 1, 0, 0; 1, 0, 1, 0, 1, 0; 5, 4, 6, 0, 0, 0) $,
  $ A $, $ I $
)

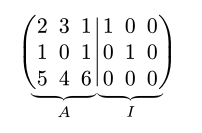
image

EDIT: This will modify the baseline of the matrix which might look odd next to matrices without an underbrace or with an overbrace. You can manually adjust it with #move(). I have also made an over-mat-function just for completeness now with automatic measuring even for matrices where one side is visually bigger.

Code and Result 
#import "@preview/xarrow:0.3.1": xarrow

#let under-mat(matrix, left, right) = context {
  let augment-row = math.mat(matrix.body.rows.first().slice(0, matrix.body.augment))
  let aug-width = measure(augment-row).width
  let rest-width = measure(matrix).width - aug-width - 15pt
  
  let lspace = math.underbrace(h(aug-width), left)
  let rspace = math.underbrace(h(rest-width), right)
  
  $
    #stack(
      spacing: -0.75em,
      matrix,
      grid(columns: 2, lspace, rspace)
    )
  $
}

#let over-mat(matrix, left, right) = context {
  let augment-row = math.mat(matrix.body.rows.first().slice(0, matrix.body.augment))
  let aug-width = measure(augment-row).width
  let rest-width = measure(matrix).width - aug-width - 15pt
  
  let lspace = math.overbrace(h(aug-width), left)
  let rspace = math.overbrace(h(rest-width), right)
  
  $
    #stack(
      grid(columns: 2, lspace, rspace),
      matrix,
    )
  $
}


$
  #under-mat(
    $ mat(augment: #3, 2, 3, 1, 1, 0, 0; 1, 0, 1, 0, 1, 0; 5, 4, 6, 0, 0, 0) $,
    $ A $, $ I $
  ) 
  xarrow("Gauss", opposite: "Jordan")
  #move(dy: -0.75em,
    over-mat(
      $ mat(
        augment: #3, 1, 0, 0, 4 slash 7, 2, -3 slash 7; 
        0, 1, 0, 1 slash 7, -1, 1 slash 7; 
        0, 0, 1, -4 slash 7, -1, 3 slash 7) $,
      $ I $, $ A^(-1) $
    ) 
  )
$

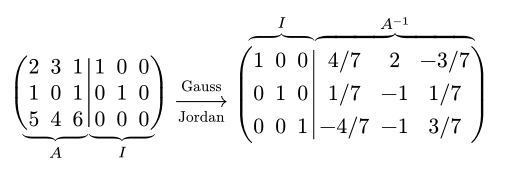
image

4 Likes
4

Thanks so much. That’s exactly what I need