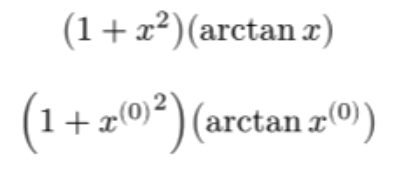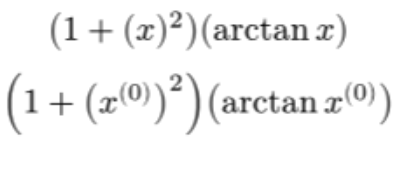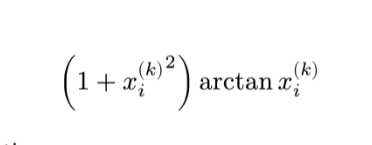How to check if a math expression ends in an exponent?

[rdong8]

#let newtonDirectionElement(x) = $(1 + #x^2)(arctan #x)$

$
    newtonDirectionElement(x)\
    newtonDirectionElement(x^((0)))
$

Result:

The superscript (0) gets messed up. However I don’t want to add parentheses in the function definition, because I don’t want them to be there even when it’s unnecessary like in the first case:

#let newtonDirectionElement(x) = $(1 + (#x)^2)(arctan #x)$

Of course I can fix this by adding the parentheses to the argument when calling the function but this adds some noise. How can I conditionally check if the given argument ends in an exponent, and then add the parentheses if needed?

[aarnent]

The following snippet should cover most common use cases:

#let newtonDirectionElement(x) = if x.func() == math.attach and x.has("t") {
  $(1 + (#x)^2)(arctan #x)$
} else {
  $(1 + #x^2)(arctan #x)$
}

[rdong8]

Thanks! Is it possible to get it to work in a nested function context? ie.

    #let newtonDirection(x) = {
      $
        (newtonDirectionElement(#x))_(i=1)^n
      $
    }

[aarnent]

I’m not quite sure what you mean. Does wrapping it in curly braces do the trick?

#let newtonDirectionElement(x) = {
  if x.func() == math.attach and x.has("t") {
    $(1 + (#x)^2)(arctan #x)$
  } else {
    $(1 + #x^2)(arctan #x)$
  }
}

[rdong8]

Ah sorry I realized that wasn’t the problem. I was trying to get it to work when the argument itself is another function call:

#let xik(i, k) = $x_#i^((#k))$

$
  newtonDirectionElement(xik(i, k))
$

However it still ends up doing the double exponent

[aarnent]

Ah I see. This should fix the issue:

#let newtonDirectionElement(x) = {
  if x.func() == math.equation {
    x = x.body
  }
  if x.func() == math.attach and x.has("t") {
    $(1 + (#x)^2)(arctan #x)$
  } else {
    $(1 + #x^2)(arctan #x)$
  }
}

The issue is that the function wasn’t expecting equations as arguments. An alternative solution would be to define xik to be

#let xik(i, k) = math.attach($x$, b: i, t: k)

[rdong8]

Many thanks!