How to have table cells of same height, because of a rowspan in first column?

[TheBigBadBoy]

In the table below, I would like the cells on the last 3 rows to have the same exact height.

table(columns: 9, stroke: (paint: gray.lighten(65%)), align: horizon,
    table.cell(colspan: 2)[Number of #acrpl("GPU")], table.vline(stroke: (paint: black)), ..range(7).map(n => [#(calc.pow(2,n))]), table.hline(stroke: (paint: black)),
    table.cell(rowspan: 3, align: horizon, rotate(-90deg, reflow: true, [Iteration time (ms)])),
    [Blocking #acs("MPI")], [136.8], [69.1], [35.9], [22.1], [14.8], [15.1], [40.8],
    [Non-blocking #acs("MPI")], [136.8], [68.7], [34.7], [18.2], [9.5], [5.6], [7.2],
    [Masked\ #acs("MPI")], [136.8], [68.6], [34.3], [17.2], [8.7], [4.4], [3.4]
  )

The output I get shows this:

[TheBigBadBoy]

How to make each grid cell take up all available space?

Sorry, I can’t find a proper and concise way to describe the problem in the title. Let me explain in detail here. I’m making a poster with many color boxes. I want all boxes aligned and fill up all available vertical space and thus there is no extra blank areas. Here is a simplified version of it: #set page(width: 300pt, height: 200pt) #set rect( inset: 8pt, fill: rgb("e4e5ea"), width: 100%, radius: 5pt, ) #grid( columns: (1fr, 1fr, 1fr), gutter: 3pt, grid.cell(rowspan: 2, rect…

Might be a good starting point, however it makes the table take the place of the whole page.

[Andrew]

Hello. I don’t know how abstracted this should be, but I think you would have to use some wrapper either way. The only other way I can think of is similar to How to distribute column widths equally for specific rows in a table? - #4 by Andrew.

#set rotate(reflow: true)

#let even-height(first, ..rest) = {
  if (
    type(first) != content
      or first.func() != table.cell
      or "rowspan" not in first.fields()
  ) {
    return arguments(first, ..rest)
  }
  let height = measure(first).height
  let rows = first.fields().rowspan
  (first,)
  rest.pos().map(block.with(height: height / rows))
}

#context table(
  columns: 9,
  stroke: gray.lighten(65%),
  align: center + horizon,
  table.header(
    table.cell(colspan: 2)[Number of GPUs],
    table.vline(stroke: (paint: black)),
    ..range(7).map(n => [#calc.pow(2, n)]),
  ),
  table.hline(stroke: black),
  ..even-height(
    table.cell(rowspan: 3, rotate(-90deg)[Iteration time (ms)]),
    [Blocking MPI],
    [136.8],
    [69.1],
    [35.9],
    [22.1],
    [14.8],
    [15.1],
    [40.8],

    [Non-blocking MPI],
    [136.8],
    [68.7],
    [34.7],
    [18.2],
    [9.5],
    [5.6],
    [7.2],

    [Masked\ MPI],
    [136.8],
    [68.6],
    [34.3],
    [17.2],
    [8.7],
    [4.4],
    [3.4],
  ),
)

You have to get the height of the first cell somehow, otherwise any ratio or fraction will be against page sizes. You can just specify absolute length to rows, and it will work, but it’s a manual value.

Here is the easiest approach: get the first tall cell, the rest of the cells, measure the total height, get the number of rows spanned, divide one by another and set the height for the rest of the cells to this.

[PgBiel]

You can use rows to set the height of rows. Here are some alternative approaches using it:

1. Guessing a fixed height for the cells (or measuring if you prefer) and using that. (Note that the last row height is repeated, so the 3 rows have the same height.)
2. Limiting the space available to the table (or using the whole remainder of your page), and using 1fr (1 fractional unit) rows which automatically split remaining space equally.

For the former, you’d use e.g. rows: (auto, 3em). For the latter, rows: (auto, 1em). Since the former one is pretty straightforward, here’s how the second one would look like.

#set page("a4", height: auto)
#block(height: 5cm, table(
  columns: 9,
  stroke: gray.lighten(65%),
  align: center + horizon,
  rows: (auto, 1fr),
  table.header(
    table.cell(colspan: 2)[Number of GPUs],
    table.vline(stroke: (paint: black)),
    ..range(7).map(n => [#calc.pow(2, n)]),
  ),
  table.hline(stroke: black),
  table.cell(rowspan: 3, rotate(-90deg, reflow: true)[Iteration time (ms)]),
  [Blocking MPI],
  [136.8],
  [69.1],
  [35.9],
  [22.1],
  [14.8],
  [15.1],
  [40.8],

  [Non-blocking MPI],
  [136.8],
  [68.7],
  [34.7],
  [18.2],
  [9.5],
  [5.6],
  [7.2],

  [Masked\ MPI],
  [136.8],
  [68.6],
  [34.3],
  [17.2],
  [8.7],
  [4.4],
  [3.4],
))

[TheBigBadBoy]

Thanks to both of you for your help!
I really thought Typst had a thing like “minimize the area of the table while maximize rows height when they are 1fr”.
I think I’ll go with the first answer though, as it provides some abstraction (and I have a few tables across my document, so I don’t feel like measuring everything). Thanks again.

[SillyFreak]

@TheBigBadBoy

minimize the area of the table while maximize rows height when they are 1fr

huh, that framing inspired me. You can actually do that*: measure how much space the table requres with auto rows, and then put it in a fitting block with 1fr rows:

#let t = table(
  columns: 9,
  // rows not specified
  stroke: (paint: gray.lighten(65%)),
  align: horizon,
  
  table.cell(colspan: 2)[Number of #acrpl("GPU")],
  table.vline(stroke: (paint: black)),
  ..range(7).map(n => [#(calc.pow(2,n))]),
  table.hline(stroke: (paint: black)),
  
  table.cell(rowspan: 3, align: horizon, rotate(-90deg, reflow: true, [Iteration time (ms)])),
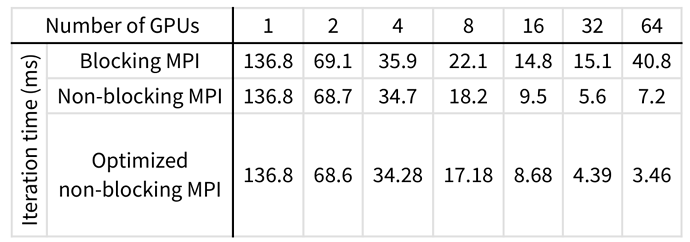
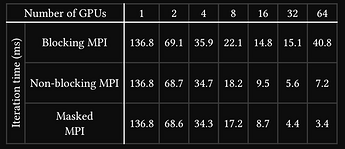
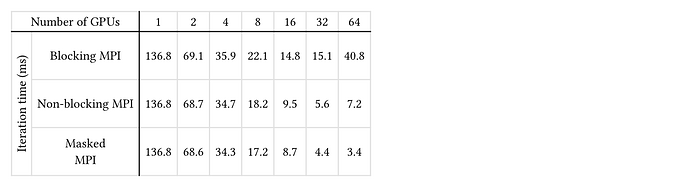
  [Blocking #acs("MPI")], [136.8], [69.1], [35.9], [22.1], [14.8], [15.1], [40.8],
  [Non-blocking #acs("MPI")], [136.8], [68.7], [34.7], [18.2], [9.5], [5.6], [7.2],
  [Masked\ #acs("MPI")], [136.8], [68.6], [34.3], [17.2], [8.7], [4.4], [3.4]
)
#layout(outer-size => {
  // measure without rows configured, but constrained by available space
  let size = measure(..outer-size, t)
  // use set rules to change rows
  set table(rows: (auto,) + 3 * (1fr,))
  // render the table in a block with fixed size, so that 1fr only fills that space
  block(..size, t)
})

* this has the problem that the table might actually need more space when row heights are distributed, so it’s still not perfect. For example, if one row was significantly taller than the others, then distributing height away from it will make it overflow. You can see that by adding lorem(20) to one of the rows.

(@Andrew’s solution seems to have the same problem, but additionally his table is generally a bit taller than necessary (when there’s actually height to distribute) because he doesn’t factor in table insets.)

I think that means that there are generally two cases:

• if the leftmost column’s height is larger than what is needed for accommodating three rows as tall as the tallest one (like your example), then my (and Andrew’s) trick works
• if the sum of the rows is taller than the leftmost column, then our tricks will no longer work, and instead the row height needs to be based on the tallest cell in all three rows