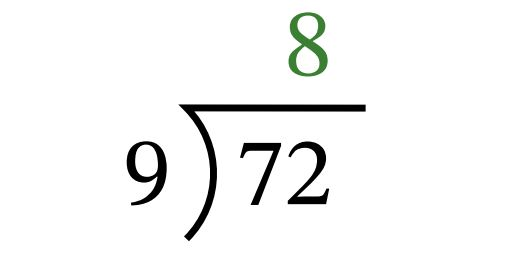Below are maths algorithms for Long Multiplication, Addition and Subtraction, and Long Division. Addition developed by @ensko and the rest modified from this.
Long Division, I cannot get to look pretty and keen on some feedback to make it look nicer:
- Clean vinculum
Some other improvements if anyone can suggest:
- Support for decimal arithmetic
Hopefully someone can help make the final one!
#set text(3em)
// convert a number to a string, split it into characters, and convert it back into digits
#let digits(x) = str(x).clusters().map(int)
#let algorithm_add(..summands) = {
assert.eq(summands.named(), (:))
// represent each summand as an array, least significant digit first
let summands = summands.pos().map(x => digits(x).rev())
let len = calc.max(..summands.map(array.len))
// do the summation, digit by digit
let columns = ()
let carry = 0
for i in range(len) {
// get all the digits
let summands = summands.map(x => x.at(i, default: none))
// calculate sum, split into ones and tens
let sum = summands.sum() + carry
let (sum, new-carry) = (calc.rem(sum, 10), int(sum/10))
// save the result, always prepending so that the most significant
// digits end up left
columns.insert(0, (
summands: summands,
sum: sum,
carry: carry,
))
carry = new-carry
}
// add a final column if there's a carry
if carry != 0 {
columns.insert(0, (
summands: (none,) * summands.len(),
sum: carry,
carry: 0,
))
}
// add a dummy column for the addition sign
columns.insert(0, none)
block(breakable: false)[
#grid(
columns: columns.len(),
inset: 0.1em,
// go through all summands
..range(summands.len()).map(r => {
// go through all columns
columns.enumerate().map(((c, col)) => {
if col == none {
// this is the first column
if r == summands.len() - 1 [+]
else []
} else {
// this is a regular column
if r == 0 and col.carry != 0 {
// first line: put the carry
place(dx: -0.15em, dy: -0.1em, text(0.3em)[#col.carry])
}
// put the digit
[#col.summands.at(r)]
}
})
}).flatten(),
grid.hline(),
// sum
..columns.enumerate().map(((c, col)) => {
if col == none []
else [#col.sum]
}),
)
]
}
#let algorithm_mult(multiplicand, multiplier) = {
// represent numbers as arrays, least significant digit first
let multiplicand-digits = digits(multiplicand).rev()
let multiplier-digits = digits(multiplier).rev()
// calculate all partial products with carry information
let partial-products = ()
for (i, mult-digit) in multiplier-digits.enumerate() {
if mult-digit == 0 {
// skip zero multipliers but maintain position
partial-products.push((digits: (0,), carries: (), offset: i))
continue
}
let product-digits = ()
let carries = ()
let carry = 0
// multiply each digit of multiplicand by current multiplier digit
for (j, digit) in multiplicand-digits.enumerate() {
let product = digit * mult-digit + carry
product-digits.push(calc.rem(product, 10))
let new-carry = int(product / 10)
// Store the carry that will be used for the NEXT position
if new-carry > 0 and j < multiplicand-digits.len() - 1 {
carries.push((pos: j + 1, value: new-carry))
}
carry = new-carry
}
// add final carry if exists
if carry > 0 {
product-digits = product-digits + digits(carry).rev()
}
partial-products.push((digits: product-digits, carries: carries, offset: i))
}
// calculate final sum by adding all partial products
let max-len = calc.max(..partial-products.map(p => p.digits.len() + p.offset))
let sum-digits = (0,) * max-len
let carry = 0
for pos in range(max-len) {
let sum = carry
for product in partial-products {
let digit-pos = pos - product.offset
if digit-pos >= 0 and digit-pos < product.digits.len() {
sum += product.digits.at(digit-pos)
}
}
sum-digits.at(pos) = calc.rem(sum, 10)
carry = int(sum / 10)
}
// Build column structure
let total-width = calc.max(multiplicand-digits.len(), multiplier-digits.len(), sum-digits.len()) + 1
let num-carry-rows = multiplier-digits.len() // One row of carries per multiplier digit
// Initialize columns
let columns = ()
for i in range(total-width) {
columns.push(())
}
// Add carry rows (above multiplicand)
for carry-row in range(num-carry-rows) {
columns.at(0).push(none) // no operator for carry rows
let multiplicand-start = total-width - multiplicand-digits.len()
// Add carries for this step - use reverse order so bottom carry row corresponds to first multiplier digit
let product-index = num-carry-rows - 1 - carry-row
if product-index < partial-products.len() {
let product = partial-products.at(product-index)
for (i, digit) in multiplicand-digits.rev().enumerate() {
let col-pos = multiplicand-start + i
let multiplicand-pos = multiplicand-digits.len() - 1 - i
// Check if there's a carry for this position in this step
let carry-value = none
for carry-info in product.carries {
if carry-info.pos == multiplicand-pos {
carry-value = carry-info.value
break
}
}
if carry-value != none {
columns.at(col-pos).push(place(dy: 0em, dx: 0.21em, text(0.3em)[#carry-value]))
} else {
columns.at(col-pos).push(none)
}
}
}
// Fill empty columns with none
for i in range(1, multiplicand-start) {
columns.at(i).push(none)
}
}
// Add multiplicand (right-aligned)
columns.at(0).push(none)
let multiplicand-start = total-width - multiplicand-digits.len()
for (i, digit) in multiplicand-digits.rev().enumerate() {
columns.at(multiplicand-start + i).push(digit)
}
// Fill empty columns with none
for i in range(1, multiplicand-start) {
columns.at(i).push(none)
}
// Add multiplier with × symbol (right-aligned)
columns.at(0).push([×])
let multiplier-start = total-width - multiplier-digits.len()
for (i, digit) in multiplier-digits.rev().enumerate() {
columns.at(multiplier-start + i).push(digit)
}
// Fill empty columns with none
for i in range(1, multiplier-start) {
columns.at(i).push(none)
}
// Add partial products (if multi-digit multiplier)
if multiplier-digits.len() > 1 {
for product in partial-products {
if product.digits != (0,) {
columns.at(0).push(none)
// Add product digits right-aligned with proper offset
let product-start = total-width - product.digits.len() - product.offset
for (i, digit) in product.digits.rev().enumerate() {
columns.at(product-start + i).push(digit)
}
// Fill empty columns with none
for i in range(1, product-start) {
columns.at(i).push(none)
}
for i in range(product-start + product.digits.len(), total-width) {
columns.at(i).push(none)
}
}
}
}
// Add final sum (right-aligned)
columns.at(0).push(none)
let sum-start = total-width - sum-digits.len()
for (i, digit) in sum-digits.rev().enumerate() {
columns.at(sum-start + i).push(digit)
}
// Fill empty columns with none
for i in range(1, sum-start) {
columns.at(i).push(none)
}
// Calculate number of rows for each column
let num-rows = columns.at(0).len()
let multiplicand-row = num-carry-rows
let multiplier-row = num-carry-rows + 1
block(breakable: false)[
#grid(
columns: total-width,
inset: (x, y) => {
// Reduce horizontal spacing for carry rows (first num-carry-rows rows)
if y < num-carry-rows {
(x: 0.05em, y: 0.15em)
} else {
0.1em
}
},
// Render all rows
..range(num-rows).map(r => {
// Add horizontal line after multiplier
if r == multiplier-row + 1 {
range(total-width).map(_ => grid.hline())
}
// Add horizontal line before sum (last row)
else if r == num-rows - 1 {
range(total-width).map(_ => grid.hline())
}
// Render row content
columns.map(col => {
let cell = col.at(r, default: none)
if cell == none { [] } else { [#cell] }
})
}).flatten()
)
]
}
#let algorithm_subtract(minuend, subtrahend) = {
// determine if result will be negative
let is-negative = minuend < subtrahend
// if result would be negative, swap the numbers
let (top-num, bottom-num) = if is-negative {
(subtrahend, minuend)
} else {
(minuend, subtrahend)
}
// represent numbers as arrays, least significant digit first
let minuend-digits = digits(top-num).rev()
let subtrahend-digits = digits(bottom-num).rev()
let max-len = calc.max(minuend-digits.len(), subtrahend-digits.len())
// pad with zeros if needed
while minuend-digits.len() < max-len {
minuend-digits.push(0)
}
while subtrahend-digits.len() < max-len {
subtrahend-digits.push(0)
}
// perform subtraction with borrowing, tracking changes
let result-digits = ()
let working-minuend = minuend-digits.map(x => x) // deep copy
let borrow-info = () // track borrowing details for each position
for i in range(max-len) {
let min-digit = working-minuend.at(i)
let sub-digit = subtrahend-digits.at(i)
// check if we need to borrow
if min-digit < sub-digit {
// find the next non-zero digit to borrow from
let borrow-pos = i + 1
let borrow-chain = () // track the chain of borrowing
// handle borrowing through zeros
while borrow-pos < max-len and working-minuend.at(borrow-pos) == 0 {
borrow-chain.push(borrow-pos)
working-minuend.at(borrow-pos) = 9
borrow-pos += 1
}
if borrow-pos < max-len {
// borrow from this position
working-minuend.at(borrow-pos) -= 1
borrow-chain.push(borrow-pos)
working-minuend.at(i) += 10
// record borrowing info for visual display
for pos in borrow-chain {
borrow-info.push((position: pos, borrowed-from: true))
}
borrow-info.push((position: i, borrowed-to: true))
}
}
// perform the subtraction
let diff = working-minuend.at(i) - sub-digit
result-digits.push(diff)
}
// remove leading zeros from result
while result-digits.len() > 1 and result-digits.at(-1) == 0 {
let _ = result-digits.pop()
}
// Build the visual representation
let total-width = max-len + 1
let has-borrows = borrow-info.len() > 0
// Initialize columns
let columns = ()
for i in range(total-width) {
columns.push(())
}
// Add borrow row (above minuend) if there are any borrows
if has-borrows {
columns.at(0).push(none)
for (i, original-digit) in minuend-digits.rev().enumerate() {
let col-pos = i + 1
let digit-pos = max-len - 1 - i
// Check if this position was borrowed from
let was-borrowed-from = original-digit != working-minuend.at(digit-pos)
if was-borrowed-from {
// Show small digit above the crossed-out original
columns.at(col-pos).push(
place(dx: 0em, dy: -0.15em, text(0.4em)[#working-minuend.at(digit-pos)])
)
} else {
columns.at(col-pos).push(none)
}
}
}
// Add minuend row (with crossed out digits where borrowed from)
columns.at(0).push(none)
for (i, original-digit) in minuend-digits.rev().enumerate() {
let col-pos = i + 1
let digit-pos = max-len - 1 - i
// Check if this position was borrowed from
let was-borrowed-from = original-digit != working-minuend.at(digit-pos)
if was-borrowed-from {
// Show crossed out original digit
columns.at(col-pos).push(text(strike[#original-digit]))
} else {
// Show original digit
columns.at(col-pos).push(original-digit)
}
}
// Add subtrahend with − symbol
columns.at(0).push([−])
for (i, digit) in subtrahend-digits.rev().enumerate() {
let col-pos = i + 1
if digit != 0 or subtrahend-digits.rev().slice(0, i+1).any(d => d != 0) {
columns.at(col-pos).push(digit)
} else {
columns.at(col-pos).push(none)
}
}
// Add result with negative sign if needed
if is-negative {
columns.at(0).push([−])
} else {
columns.at(0).push(none)
}
// Add result digits
for (i, digit) in result-digits.rev().enumerate() {
let col-pos = max-len - result-digits.len() + i + 1
columns.at(col-pos).push(digit)
}
// Fill empty columns in result row
for i in range(1, max-len - result-digits.len() + 1) {
columns.at(i).push(none)
}
// Calculate number of rows
let num-rows = columns.at(0).len()
let subtrahend-row = if has-borrows { 2 } else { 1 }
block(breakable: false)[
#grid(
columns: total-width,
inset: (x, y) => {
// Reduce spacing for borrow row
if y == 0 and has-borrows {
(x: 0.05em, y: 0.05em)
} else {
0.1em
}
},
// Render all rows
..range(num-rows).map(r => {
// Add horizontal line after subtrahend
if r == subtrahend-row + 1 {
range(total-width).map(_ => grid.hline())
}
// Render row content
columns.map(col => {
let cell = col.at(r, default: none)
if cell == none { [] } else { [#cell] }
})
}).flatten()
)
]
}
// Long division algorithm with proper step-by-step display
#let algorithm_long_divide(dividend, divisor) = {
let dividend-digits = digits(dividend)
let divisor-int = divisor
// Track the division process
let quotient-digits = ()
let steps = () // Each step contains: partial-dividend, quotient-digit, subtraction, remainder, bring-down-digit
let current-dividend = 0
let working-dividend = 0
// Process each digit of the dividend
for (i, digit) in dividend-digits.enumerate() {
// Bring down the next digit
working-dividend = current-dividend * 10 + digit
// Calculate quotient digit (0 if working dividend is smaller than divisor)
let quotient-digit = if working-dividend >= divisor-int {
calc.floor(working-dividend / divisor-int)
} else { 0 }
quotient-digits.push(quotient-digit)
// Calculate what we subtract
let subtraction = quotient-digit * divisor-int
// Calculate remainder
let remainder = working-dividend - subtraction
// Calculate the rightmost position of this working dividend
let working-end-pos = i
let working-start-pos = working-end-pos - str(working-dividend).len() + 1
// Store step information
steps.push((
working-dividend: working-dividend,
quotient-digit: quotient-digit,
subtraction: subtraction,
remainder: remainder,
position: i,
brought-down: digit,
working-start-pos: working-start-pos,
working-end-pos: working-end-pos
))
// The remainder becomes the start of the next division
current-dividend = remainder
}
// Remove leading zeros from quotient
while quotient-digits.len() > 1 and quotient-digits.first() == 0 {
quotient-digits = quotient-digits.slice(1)
}
// Calculate layout dimensions
let dividend-width = dividend-digits.len()
let quotient-width = quotient-digits.len()
let divisor-width = str(divisor).len()
let digit-width = 0.6em
let divisor-space = divisor-width * digit-width + 0.3em
block(breakable: false)[
#set align(left)
// Top section: divisor, division bar, quotient, and dividend
#stack(
dir: ttb,
spacing: 0.15em,
// Quotient line with remainder if any - right aligned above dividend
stack(
dir: ltr,
spacing: 0em,
h(divisor-space + 0.5em), // Space for divisor and division symbol
// Add spacing to right-align quotient above dividend
h((dividend-digits.len() - quotient-digits.len()) * digit-width),
..quotient-digits.map(d => box(width: digit-width, align(center)[#d])),
if steps.last().remainder > 0 {
h(0.3em)
text(0.9em)[r]
text(size: 1em)[#steps.last().remainder]
}
),
// Division symbol, horizontal line, and dividend (all on same line)
stack(
dir: ltr,
spacing: 0.05em,
box(width: divisor-space - 0.1em, align(right)[#str(divisor)]),
box(width: 0.5em, align(center)[)]),
stack(
dir: ttb,
spacing: 0em,
line(length: dividend-digits.len() * digit-width, stroke: 0.8pt),
stack(
dir: ltr,
spacing: 0em,
..dividend-digits.map(d => box(width: digit-width, align(center)[#d]))
)
)
),
// Working steps
..steps.enumerate().map(((step-idx, step)) => {
if step.quotient-digit > 0 { // Only show steps where we actually divide
let base-indent = divisor-space + 0.5em
// Position the subtraction to align with the working dividend
let step-indent = base-indent + step.working-start-pos * digit-width
stack(
dir: ttb,
spacing: 0.05em,
// Subtraction line (what we multiply and subtract)
stack(
dir: ltr,
spacing: 0em,
h(step-indent),
..digits(step.subtraction).map(d => box(width: digit-width, align(center)[#d]))
),
// Underline for subtraction
stack(
dir: ltr,
spacing: 0em,
h(step-indent),
line(length: str(step.subtraction).len() * digit-width, stroke: 0.6pt)
),
// Remainder and brought down digit (if applicable)
if step-idx < steps.len() - 1 {
let next-step = steps.at(step-idx + 1)
let remainder-digits = if step.remainder == 0 { () } else { digits(step.remainder) }
let combined-digits = remainder-digits + (next-step.brought-down,)
// Position the combined number to align properly
// The remainder should align right under the subtraction, then bring down next digit
let remainder-start = step.working-end-pos - remainder-digits.len() + 1
let combined-indent = base-indent + remainder-start * digit-width
stack(
dir: ltr,
spacing: 0em,
h(combined-indent),
..combined-digits.map(d => box(width: digit-width, align(center)[#d]))
)
} else if step.remainder > 0 {
// Final remainder - align with the subtraction
let remainder-digits = digits(step.remainder)
let remainder-indent = step-indent + (str(step.subtraction).len() - remainder-digits.len()) * digit-width
stack(
dir: ltr,
spacing: 0em,
h(remainder-indent),
..remainder-digits.map(d => box(width: digit-width, align(center)[#d]))
)
}
)
}
}).filter(x => x != none)
)
]
}
#algorithm_add(744, 2480)
#algorithm_mult(409,49)
#algorithm_subtract(542, 1876)
#algorithm_subtract(50, 123)
// Test cases
#algorithm_long_divide(84, 4)
#v(1em)
#algorithm_long_divide(19, 12)
#v(1em)
#algorithm_long_divide(2847, 23)